DIAMAGNÉTISME

DIAMAGNÉTISME

Les corps qui, contrairement aux substances dites magnétiques, possèdent une perméabilité magnétique 猪 (rapport entre le vecteur induction Bet le vecteur champ H 轢) inférieure à celle du vide sont dits diamagnétiques. Les lignes de force d’un champ magnétique sont alors repoussées vers l’extérieur; les points par lesquels pénètrent les lignes de force s’aimantent positivement, alors que ceux par lesquels elles sortent s’aimantent négativement.

Il en résulte l’apparition d’un moment magnétique minduit par le champ magnétique et qui lui est opposé (ce moment magnétique disparaît avec la cause excitatrice, contrairement à ce qui se passe dans le cas des corps ferromagnétiques).

Le plus souvent, ce moment induit est proportionnel au champ inducteur:

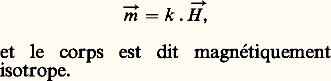Le coefficient de proportionnalité qui caractérise le corps est appelé susceptibilité magnétique. Il est négatif et est relié à la perméabilité par la relation 猪 = 1 + 4 神 k (systèmes non rationalisés) ou 猪 = 1 + k (système Giorgi rationalisé, ou S.I.).

Ce moment induit, opposé au champ inducteur, est lié à l’apparition de forces tendant à repousser le corps vers la région des champs faibles. Ces forces sont toujours très petites: la répulsion due à un électro-aimant produisant un champ d’un million d’ampères par mètre sur un gramme de substance diamagnétique est de l’ordre de 10^-5 newton, ce qui explique pourquoi le diamagnétisme est demeuré longtemps inaperçu.

La quasi-totalité des molécules organiques, la plupart des gaz (l’oxygène et l’oxyde d’azote, NO, font exception), l’eau, les acides, les éléments chimiques non métalliques et de nombreux métaux sont diamagnétiques.

La susceptibilité magnétique d’une quantité donnée de substance diamagnétique est, à de rares exceptions près (métaux, bismuth, graphite), pratiquement indépendante de la température (loi de Curie).

1. Définitions

Dans le cas des substances homogènes, il est commode de définir la susceptibilité volumique , ou susceptibilité par unité de volume, et la susceptibilité massique 﨑 (appelée souvent susceptibilité spécifique), ou susceptibilité par unité de masse. Ces grandeurs sont liées à la susceptibilité k par les relations:

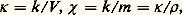où V , m et 福 désignent respectivement le volume, la masse et la masse volumique de la substance.

On caractérise les atomes et les molécules par les susceptibilités atomiques 﨑 ^A et molaires 﨑 ^M; ce sont les susceptibilités d’un atome-gramme ou d’une mole:

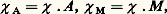A désignant la masse atomique d’un atome et M la masse molaire d’une molécule.

Ces susceptibilités sont encore, le plus souvent, exprimées en u.é.m. C.G.S.; on passe aux susceptibilités du système S.I. en utilisant la relation:

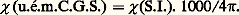Les susceptibilités diamagnétiques massiques, sont, à de rares exceptions près, comprises entre 漣 0,2.10^-6 et 漣 0,9 憐 10^-6.

Pierre Curie a montré, en 1895, que les susceptibilités diamagnétiques massiques de la plupart des molécules sont pratiquement indépendantes de la température (tabl. 1).

2. Anisotropie magnétique

En réalité, le moment induit n’est pas toujours colinéaire au champ inducteur, en particulier pour les substances se présentant sous la forme de monocristaux. Les propriétés magnétiques de ces corps, dits anisotropes, sont alors caractérisées par un ensemble de neuf susceptibilités 﨑 ^xx, 﨑 ^xy..., les composantes m ^x, m ^y, m ^z du moment induit étant reliées aux composantes H ^x, H ^y, H ^z du champ par les relations:

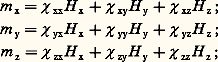ce que l’on écrit sous forme tensorielle:

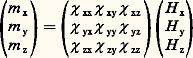ou, plus simplement: ゆ = 﨑 練 で.

Le tableau carré 﨑 des 﨑 ^ij est appelé tenseur des susceptibilités. C’est un tenseur du second ordre symétrique ( 﨑 ^ij = 﨑 ^ji ).

Il existe trois axes triorthogonaux, OX, OY, OZ, appelés axes principaux d’aimantation, pour lesquels le moment induit est colinéaire au champ inducteur. Si l’on se réfère à ce nouveau système d’axes, le tenseur des susceptibilités se réduit à sa forme diagonale:

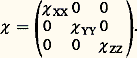Il est généralement plus commode de caractériser le tenseur des susceptibilités par la connaissance des axes principaux d’aimantation et des trois susceptibilités principales ( 﨑 ^XX, 﨑 ^YY, 﨑 ^ZZ), plutôt que par les neuf composantes du tenseur dans un système d’axes quelconque.

Lorsque le champ est dans une direction faisant les angles 見 , 廓 et 塚 avec les trois axes OX, OY et OZ, la projection du moment sur la direction du champ est:

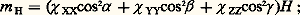on en déduit la susceptibilité dans cette direction:

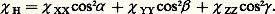On peut construire le moment induit ゆ en décomposant le champ で suivant ses composantes et en recomposant les aimantations induites correspondantes (fig. 1).

Si l’on fait une mesure sur un grand nombre de cristallites orientées au hasard, on obtient une susceptibilité moyenne 﨑 :

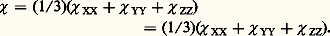Les quantités entre parenthèses représentent la somme des éléments diagonaux, ou trace, du tenseur. Cette trace est un invariant tensoriel et ne dépend pas des axes de référence choisis.

Les mesures effectuées sur des liquides ou sur des gaz, dans lesquels les molécules sont animées de mouvements de rotation rapides, conduisent également à une susceptibilité moyenne.

Le tableau 2 rassemble les caractéristiques du tenseur de susceptibilité liées à la symétrie pour les différents systèmes cristallins.

Les états mésomorphes, nématiques et smectiques montrent également une anisotropie diamagnétique, le diamagnétisme le plus faible correspondant généralement à la plus grande dimension de la molécule.

Krishnan et Lonsdale ont montré comment on pouvait passer des susceptibilités principales cristallines aux susceptibilités principales moléculaires. Les molécules possédant les anisotropies magnétiques les plus importantes sont les molécules aromatiques, pour lesquelles les susceptibilités principales 﨑 ^XX et 﨑 ^YY dans le plan moléculaire sont pratiquement égales et inférieures en valeur absolue à la susceptibilité 﨑 ^ZZ perpendiculaire à ce plan. On définit alors l’anisotropie magnétique K par la relation (tabl. 3):

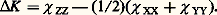Les susceptibilités principales des cristaux varient légèrement avec la température par suite de la modification de la position des molécules dans la maille cristalline.

3. Théorie du diamagnétisme

Paul Langevin a montré, en 1905, que le diamagnétisme est dû au mouvement orbital des électrons autour des noyaux. C’est donc une propriété générale de la matière, mais elle peut être masquée par le paramagnétisme ou par le ferromagnétisme dus à la présence de spins électroniques non appariés. La susceptibilité est alors positive et sa valeur absolue est de dix à cent fois plus élevée pour le paramagnétisme, et beaucoup plus grande encore dans le cas du ferromagnétisme.

Si l’on admet, avec Langevin, que les atomes sont formés d’électrons décrivant des trajectoires circulaires de rayon r ^k , la mécanique classique conduit à l’expression suivante, pour la contribution de l’électron k dont l’orbite est perpendiculaire à la direction Oz du champ magnétique:

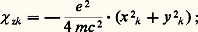où m est la masse d’un électron; x ^k et y ^k , les coordonnées de l’électron k ; c , la vitesse de la lumière.

La susceptibilité moyenne d’un ensemble de N atomes orientés au hasard est alors:

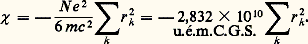Remarquons que ce résultat découle en fait de l’hypothèse (quantique) de l’existence d’orbites circulaires stables, car miss Van Leuwen a montré qu’en toute rigueur la mécanique classique devait conduire à un diamagnétisme nul.

La mécanique quantique a permis de préciser la théorie. On calcule l’expression de l’énergie E d’un système en présence d’un champ magnétique で en utilisant soit la méthode des perturbations, soit la méthode des variations, et on peut en déduire alors la susceptibilité grâce à la formule:

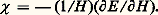La première de ces méthodes a conduit Van Vleck à l’expression suivante, pour une molécule se trouvant dans l’état fondamental d’énergie E ⁰ caractérisé par la fonction d’onde 祥 ⁰ lorsque le champ magnétique est dirigé suivant l’axe Oz:

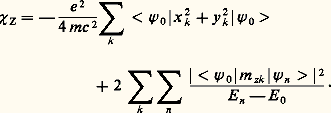Le premier terme est la traduction quantique de la formule de Langevin; le symbole 麗 祥 ⁰ |x ^2k + y ^2k | 祥 ⁰ 礪 désigne la valeur moyenne quantique de l’expression x ^2k + y ^2k . Le second, appelé terme de haute fréquence, est dû à la modification de la fonction d’onde 祥 ⁰ par le champ magnétique. Son calcul est difficile, car on ignore presque toujours l’expression des fonctions d’onde 祥 ⁿ et les énergies E ⁿ des états excités. Le symbole 麗 祥 ⁰|m ^zk | 祥 ⁿ 礪 désigne un élément non diagonal de la matrice, représentant la composante du moment magnétique suivant l’axe Oz.

La méthode de Hartree-Fock couplée (dans laquelle le champ autocohérent tient compte du champ magnétique) permet de calculer les susceptibilités magnétiques de petites molécules (par exemple H²O) avec une précision de quelques pourcents à la condition d’utiliser une base suffisamment étendue (trois fois la base minimale) et bien adaptée à la perturbation. Cependant, les résultats sont sensibles au choix de l’origine des coordonnées, ce qui rend difficile son extension aux molécules de plus grandes dimensions. L’utilisation d’une base d’orbitales atomiques particulières dites «invariantes de jauge» élimine cet inconvénient, mais allonge les calculs.

On peut considérer, en première approximation, le diamagnétisme comme une propriété des atomes. L’état de combinaison chimique intervient relativement peu, et les interactions entre les molécules encore moins. Il s’ensuit que la susceptibilité massique d’un mélange d’une masse m ¹ d’un corps de susceptibilité massique 﨑 ¹ et d’une masse m ² d’un corps de susceptibilité massique 﨑 ² etc. est donnée avec une bonne précision par la «loi des mélanges»:

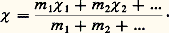Le peu d’influence de l’état de combinaison et des interactions moléculaires explique, en partie, l’invariance du diamagnétisme avec la température.

4. Loi d’additivité

Paul Pascal a montré, en 1910, que les susceptibilités diamagnétiques molaires pouvaient être calculées en utilisant une loi d’additivité de la forme:

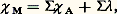la susceptibilité molaire 﨑 ^M étant égale à la somme des susceptibilités des atomes qui la constituent, additionnée, le cas échéant, d’incréments caractérisant des éléments de structure particuliers de la molécule.

Les susceptibilités atomiques 﨑 ^A intervenant dans la formule précédente résultent d’un découpage des susceptibilités expérimentales (tabl. 4).

C’est ainsi que l’on calculera pour le diméthyl-2-5 heptène-4:

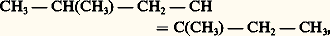qui possède 9 atomes de carbone, 18 atomes d’hydrogène, une liaison éthylénique C = C et 4 groupements CH³:

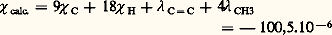alors que la valeur expérimentale est 漣 100,6.10^-6.

Le tableau 5 permet de comparer les susceptibilités mesurées 﨑 ^mes. aux susceptibilités calculées à l’aide de la systématique précédente.

Dans le cas des composés minéraux, les lois d’additivité proposées semblent conduire à un moins bon accord que pour les molécules organiques. Il est possible que ce désaccord provienne, en réalité, des difficultés expérimentales rencontrées dans la purification des substances minérales.

On peut donc calculer, a priori, la susceptibilité diamagnétique d’un composé donné. Un tel calcul est utilisé couramment pour connaître le diamagnétisme sous-jacent d’un composé paramagnétique (sel minéral ou radical libre) ou encore pour mettre en évidence les écarts à la loi d’additivité qui révèlent des particularités structurales. C’est ainsi que, dans le cas des hydrocarbures aromatiques, la susceptibilité mesurée expérimentalement est beaucoup plus importante (en valeur absolue) que la susceptibilité que l’on peut calculer en utilisant une formule classique de Kekulé. La différence:

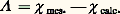est une mesure de la délocalisation électronique, importante dans ces molécules aromatiques. Le tableau 6 montre que cet incrément 炙 est approximativement proportionnel au nombre de noyaux aromatiques de la molécule considérée.

Cette exaltation du diamagnétisme est liée à l’anisotropie diamagnétique de ces molécules, car elle correspond pratiquement à l’exaltation de la seule susceptibilité 﨑 ^ZZ perpendiculaire au plan moléculaire. Si l’anisotropie de ces molécules ne provenait que de cette exaltation, on devrait avoir:

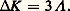En fait, il faut également tenir compte de l’anisotropie des liaisons 靖 et des électrons 神 localisés.

Linus Pauling a donné de cette propriété une explication simple: elle est due à la circulation des électrons 神 autour des cycles aromatiques. D’ailleurs, si on calcule l’anisotropie correspondant à cette circulation à l’aide de la formule de Langevin, on obtient:

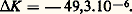Une théorie quantique a été donnée par Fritz London.

L’étude de ces composés aromatiques constitue un exemple de la contribution que peut apporter le diamagnétisme à la connaissance des structures moléculaires. L’interprétation du diamagnétisme, du paramagnétisme et du ferromagnétisme, en vue de l’étude des structures chimiques, constitue ce que l’on appelle la magnétochimie.

5. Mesure des susceptibilités diamagnétiques

La plupart des appareils utilisés se ramènent à la mesure des effets mécaniques (forces ou couples) d’un champ magnétique sur une substance. On peut également utiliser les effets produits par une substance diamagnétique dans une bobine parcourue par un courant alternatif (modification de différence de potentiel ou de fréquence). Dans tous les cas, la difficulté réside dans la petitesse des effets à mesurer et dans l’élimination des impuretés ferro- et paramagnétiques.

Effets mécaniques d’un champ magnétique sur une substance

Lorsqu’une substance diamagnétique est suspendue dans un champ magnétique, on peut observer:

a ) Une force tendant à la repousser vers la région des champs faibles. Par exemple, si un échantillon ponctuel de masse m est placé en O dans un champ magnétique で parallèle à Oy (fig. 2), il est soumis à une force づ^x dirigée parallèlement à l’axe Ox et égale à:

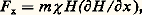﨑 étant la susceptibilité massique dans la direction Oy.

Dans un champ uniforme ( 煉 H / 煉 x = 0), la substance n’est soumise à aucune force.

Le plus souvent, ces mesures sont effectuées dans l’air, et la force effectivement mesurée est alors la différence algébrique entre la force F ^x et la force qui aurait agi sur le volume d’air déplacé:

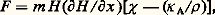où 福 est la masse spécifique de la substance et 﨑 ^A la susceptibilité volumique de l’air. Il faut noter que l’air est paramagnétique et que sa susceptibilité varie fortement avec la température; dans les conditions habituelles de mesure (1 atmosphère; 20 ⁰C), 﨑 ^A = 0,029.10^-6 cm^-3.

b ) Un couple lié à l’anisotropie magnétique; un cristal suspendu suivant l’axe principal d’aimantation OZ dans un champ magnétique uniforme horizontal d’intensité H faisant avec l’axe de plus grande susceptibilité OX ( 﨑 ^XX 礪 﨑 ^YY en valeur algébrique) l’angle est soumis à un couple (fig. 3).

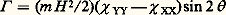( 﨑 ^xx et 﨑 ^yy sont les susceptibilités massiques).

L’équilibre a lieu lorsque = 0: l’axe de plus grande susceptibilité (en valeur algébrique) est alors parallèle au champ. Le couple est maximal lorsque = 45⁰.

c ) Un couple lié à la fois à la forme de l’échantillon et à l’hétérogénéité du champ. Un tel couple est toujours gênant pour les mesures; on cherche donc à l’éliminer, soit en utilisant des échantillons de forme cylindrique (mesure d’une susceptibilité), soit en plaçant l’échantillon dans un champ uniforme (mesure des anisotropies).

Mesure d’une susceptibilité moyenne

Un grand nombre de procédés ingénieux ont été proposés pour la mesure des forces; on décrira seulement deux des appareils les plus utilisés.

Dans l’appareil de Weiss, Foex et Forrer , la substance (échantillon polycristallin ou liquide) est placée dans une coupelle à l’extrémité d’un pendule de translation léger suspendu à un bâti exempt de vibrations. À l’autre extrémité du pendule, une bobine se déplace dans l’entrefer d’un petit aimant permanent (les arrivées de courant peuvent être constituées par deux des fils de suspension en argent).

Un électro-aimant puissant est placé de telle sorte que la quantité H ( 煉 H / 煉 x ) ait sa valeur maximale et soit pratiquement constante dans le volume où est située la coupelle (méthode de Faraday). On compense la force F ainsi produite par une force électromagnétique obtenue en faisant passer un courant I dans la bobine. Lorsque les deux forces s’équilibrent exactement, le courant I est proportionnel à F .

La quantité H ( 煉 H / 煉 x ) étant difficile à déterminer directement, on fait des mesures relatives en utilisant l’eau comme composé de référence.

On détermine alors successivement les intensités I , I ⁰ et i permettant d’équilibrer les forces F , F ⁰ et f agissant respectivement: sur la coupelle contenant m gramme de substance de susceptibilité massique 﨑 et de masse spécifique 福 ; sur la coupelle contenant m ⁰ gramme de composé de référence de susceptibilité massique 﨑 ⁰ et de masse spécifique 福 ⁰; sur la coupelle vide.

Si les mesures ont été effectuées dans l’air, on peut écrire:

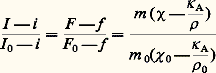d’où:

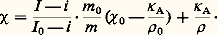Dans l’appareil de Gouy-Pascal , l’échantillon (de susceptibilité massique 﨑 ), de préférence liquide ou éventuellement polycristallin finement pulvérisé, est introduit dans un tube cylindrique. La partie supérieure de cet échantillon est placée dans le champ maximal で d’un électro-aimant puissant, la partie inférieure se trouvant dans un champ で⁰ beaucoup plus petit.

L’intégration de l’expression différentielle de la force:

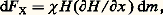conduit à l’expression:

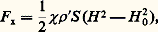ou, en tenant compte de la correction due à l’air:

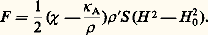Dans ces deux dernières expressions, S désigne la section du tube, 福 la masse spécifique de l’échantillon et 福 sa masse spécifique apparente (dans le cas des liquides 福 = 福 ).

Les mesures sont relatives: on mesure, à l’aide d’une balance, les forces F , F ⁰ et f agissant respectivement sur le tube contenant la substance, sur le tube contenant le même volume de liquide de référence et sur le tube vide. On en déduit:

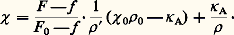Lorsqu’il n’y a pas assez de substance pour mesurer les forces, on peut immerger celle-ci dans des liquides de composition variée jusqu’à ce qu’un champ magnétique ne produise plus aucun déplacement: les susceptibilités volumiques de la substance et de la solution sont alors égales.

Mesure d’une anisotropie magnétique

Lorsqu’il s’agit de cristaux anisotropes, on peut déterminer les susceptibilités principales à l’aide d’un appareil analogue aux précédents; cependant, la mesure des couples de torsion préconisée par Krishnan donne des résultats plus précis.

Le cristal est suspendu par un point de colle à un fil de quartz très fin (de 5 à 20 猪m environ), de préférence suivant un axe principal d’aimantation, OZ par exemple.

La mesure de la modification de la période d’oscillation créée par un champ magnétique uniforme permet de déduire la différence des deux susceptibilités principales dans le plan d’oscillation ( 﨑 ^YY 漣 﨑 ^ZZ); mais la méthode suivante, qui consiste à déterminer le couple magnétique maximal, donne de meilleurs résultats.

Le cristal est placé de telle sorte que la plus grande susceptibilité (en valeur algébrique) soit parallèle au champ (le couple magnétique est alors nul), et on fait tourner l’extrémité supérieure du fil de quartz d’un angle 見 . Le cristal, qui est soumis au couple magnétique, tourne alors d’un angle (inférieur à 見 ). Si l’on augmente progressivement 見 , on constate que, pour une certaine valeur critique 見 ^c, le couple mécanique n’est plus équilibré par le couple magnétique; le cristal effectue alors une série de rapides oscillations: la position pour laquelle le couple magnétique était maximal ( = 見 /4) a été dépassée. On peut alors écrire:

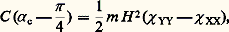où C est la constante de torsion du fil. On l’élimine ainsi que le champ magnétique en effectuant des mesures relatives. De telles mesures peuvent donner successivement les valeurs des différences 﨑 ^YY 漣 﨑 ^XX, 﨑 ^XX 漣 﨑 ^ZZ, 﨑 ^ZZ 漣 﨑 ^YY, mais on ne peut passer de ces différences aux susceptibilités principales 﨑 ^XX, 﨑 ^YY et 﨑 ^ZZ que si l’on connaît soit une de ces susceptibilités principales, soit la susceptibilité moyenne:

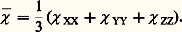La mesure des anisotropies magnétiques est un travail délicat. Une des difficultés majeures réside dans l’obtention de monocristaux de dimensions suffisantes (quelques millimètres).

Les anisotropies magnétiques de molécules possédant un moment dipolaire électrique non nul peuvent également être déduites des perturbations créées par un champ magnétique sur leur spectre de rotation à l’état gazeux (effet Zeeman moléculaire rotationnel). Ce procédé est particulièrement utile dans le cas des composés non cristallisés.

6. Diamagnétisme des «électrons libres»

Les composés à structure métallique, c’est-à-dire ceux que l’on peut considérer en première approximation comme formés d’un nuage d’électrons gravitant autour d’un ensemble périodique d’ions positifs, possèdent des propriétés caractéristiques: en particulier, leur susceptibilité diamagnétique est une fonction de la température, et, à basse température, une fonction du champ inducteur (effet Haas-Van Alphen).

C’est dans cette catégorie que l’on doit placer le graphite, qui est le composé qui possède de loin le plus grand diamagnétisme (environ dix fois les valeurs habituelles à la température ordinaire; sa susceptibilité massique est 﨑 = 漣 7,2.10^-6 à 292 K).

Son anisotropie est élevée, la susceptibilité parallèle aux plans réticulaires du graphite étant indépendante de la température et d’un ordre de grandeur classique, 﨑 ^// = 漣 0,3.10^-6, alors que la susceptibilité dans la direction perpendiculaire à ces plans, 﨑 size=1^旅, est très élevée et dépend fortement de la température (fig. 4).

On peut interpréter ces valeurs en admettant l’existence d’un «gaz d’électrons» à deux dimensions dont les effets se reportent uniquement sur la susceptibilité 﨑 size=1^旅.

Alors que la mécanique classique conduisait, pour les électrons libres, à un diamagnétisme nul, Landau a montré que la mécanique quantique permettait de prévoir un diamagnétisme important. Ce diamagnétisme est lié au fait que les niveaux d’énergie continus d’un ensemble d’électrons libres viennent se rassembler en niveaux discrets en présence d’un champ magnétique, leurs énergies étant données par l’expression:

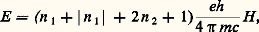n ¹ et n ² étant des nombres entiers. (On peut mettre en évidence les transitions entre deux niveaux successifs: c’est le phénomène de résonance cyclotronique.)

Le peuplement de ces niveaux est, d’une part, fonction de la température (ce qui explique la variation thermique des susceptibilités), d’autre part, fonction du champ (ce qui permet d’interpréter l’effet Haas-Van Alphen).

En réalité, le modèle précédent doit être modifié pour tenir compte du potentiel périodique du réseau. Une méthode simple consiste à remplacer la masse de l’électron par une «masse effective» caractéristique du composé étudié.

Il faut ajouter à ce diamagnétisme un paramagnétisme lié aux électrons de conduction et, bien entendu, le magnétisme des ions formant le réseau. Suivant que la somme de ces termes est négative ou positive, les composés de ce type sont diamagnétiques ou paramagnétiques.

diamagnétisme [ djamaɲetism ] n. m.

• 1849; de dia- et magnétisme

♦ Phys. Propriété d'une substance dont l'aimantation est colinéaire au champ magnétique inducteur et de sens opposé.

● diamagnétisme nom masculin Propriétés des substances dont l'aimantation induite est de sens opposé à celui du champ inducteur.

⇒DIAMAGNÉTISME, subst. masc.

PHYS. Propriété des substances qui, soumises à un champ magnétique, prennent une aimantation proportionnelle au champ, mais plus faible et dirigée en sens inverse. Il [Faraday] observa que le prisme s'orientait, non pas suivant les lignes de force, comme l'aurait fait un prisme semblable en fer, mais perpendiculairement à ces lignes. Des sphères de la même matière étaient repoussées hors du champ. C'était la découverte du diamagnétisme, phénomène entrevu à plusieurs reprises, depuis le XVIII^e siècle, notamment par A.-C. Becquerel, mais peu étudié et mal compris (Hist. gén. sc., t. 3, vol. 1, 1961, p. 224).

Prononc. :[]. Étymol. et Hist. 1858 (LITTRÉ-ROBIN). Dér. de magnétisme; préf. di-.

diamagnétisme [djamaɲetism] n. m.

ÉTYM. 1858, de dia-, et magnétisme.

❖

♦ Sc. Ensemble de phénomènes produits par les corps diamagnétiques.

Encyclopédie Universelle. 2012.